Hình học không gian là một “nỗi ám ảnh” đối với học sinh. Để giải quyết những bài toán hình học khó nhằn này đòi học bạn phải có một bộ óc tưởng tưởng và nắm vững các công thức nền tảng. Vậy làm sao để giỏi hình học không gian? Hãy cùng theo dõi bài viết sau, Toán Tuổi Thơ sẽ bật mí cho bạn những phương pháp học giỏi toán hình học không gian nhanh chóng nhất.
Hình học không gian là gì?
Hình học không gian là một nhánh của hình học chuyên nghiên cứu các hình khối ba chiều trong không gian. Khác với hình học phẳng chỉ xem xét các đối tượng trong hai chiều (chiều dài và chiều rộng), hình học không gian quan tâm đến các đối tượng có thêm chiều cao (hoặc chiều sâu).
Một số khái niệm cơ bản trong hình học không gian bao gồm:
- Điểm (Point): Một điểm không có kích thước, chỉ xác định vị trí trong không gian.
- Đường thẳng (Line): Một đường thẳng kéo dài vô hạn về cả hai phía, không có độ dày và chỉ có một chiều.
- Mặt phẳng (Plane): Một mặt phẳng kéo dài vô hạn theo hai chiều (dài và rộng), không có độ dày.
- Hình khối (Solid): Các đối tượng ba chiều như hình hộp chữ nhật, hình lập phương, hình cầu, hình trụ, hình nón, v.v.

Một số tính chất và công thức thường được sử dụng trong hình học không gian:
- Diện tích bề mặt: Tổng diện tích các mặt ngoài của một hình khối.
- Thể tích: Lượng không gian mà một hình khối chiếm.
- Đường chéo không gian: Đoạn thẳng nối hai điểm không thuộc cùng một mặt phẳng trong một hình khối.
Hình học không gian có ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, kỹ thuật, vật lý, và nhiều ngành khoa học khác.
Lý do nhiều người không học giỏi hình học không gian
Có nhiều lý do khiến nhiều người gặp khó khăn trong việc học hình học không gian. Dưới đây là một số nguyên nhân chính:
- Khó khăn trong việc hình dung không gian: Hình học không gian yêu cầu khả năng tưởng tượng và hình dung các đối tượng ba chiều, điều này có thể gây khó khăn cho nhiều người, đặc biệt là khi họ đã quen với các đối tượng hai chiều.
- Thiếu nền tảng cơ bản: Hình học không gian đòi hỏi kiến thức nền tảng vững chắc từ hình học phẳng và các khái niệm toán học cơ bản. Nếu học sinh không nắm vững những kiến thức này, họ sẽ gặp khó khăn khi tiếp cận với hình học không gian.
- Phức tạp trong tính toán: Các bài toán trong hình học không gian thường phức tạp hơn với nhiều bước tính toán và công thức cần phải nhớ. Điều này có thể khiến học sinh cảm thấy quá tải và dễ nản lòng.
- Phương pháp giảng dạy chưa hiệu quả: Cách giảng dạy không phù hợp hoặc không tận dụng các công cụ trực quan và thực hành có thể khiến học sinh không hiểu sâu về các khái niệm trong hình học không gian.
- Thiếu thực hành và ứng dụng thực tiễn: Hình học không gian thường không được liên kết chặt chẽ với các ứng dụng thực tiễn trong cuộc sống hàng ngày. Thiếu sự liên hệ này có thể làm giảm sự hứng thú và động lực học tập của học sinh.
- Áp lực tâm lý và sợ hãi: Một số học sinh có thể bị áp lực tâm lý khi đối diện với các môn học mà họ cảm thấy khó khăn. Sự sợ hãi này có thể làm giảm khả năng tiếp thu và xử lý thông tin mới.

Để cải thiện việc học hình học không gian, cần áp dụng các phương pháp giảng dạy sáng tạo và trực quan, khuyến khích học sinh thực hành nhiều và tạo sự liên kết với các ứng dụng thực tiễn. Sự hỗ trợ từ giáo viên và phụ huynh cũng đóng vai trò quan trọng trong việc giúp học sinh vượt qua khó khăn và xây dựng tự tin trong môn học này.
Làm sao để giỏi hình học không gian?
Làm sao để giỏi hình học không gian là thắc mắc của nhiều học sinh hiện nay. Dưới đây là một số phương pháp giúp bạn cải thiện môn học này.
Nắm chắc lý thuyết
Hiểu rõ các khái niệm và định lý cơ bản là nền tảng để bạn có thể giải quyết các bài tập và vấn đề phức tạp. Hãy đảm bảo rằng bạn nắm vững các công thức tính diện tích, thể tích và các tính chất của các hình khối. Điều này giúp bạn dễ dàng áp dụng vào thực tế và giải bài tập hiệu quả.

Tập nhìn hình
Khả năng tưởng tượng các đối tượng ba chiều là rất quan trọng trong hình học không gian. Tập nhìn hình sẽ giúp bạn dễ dàng hình dung các hình khối và mối quan hệ giữa chúng. Bạn có thể sử dụng các mô hình 3D, phần mềm hỗ trợ hoặc thực hành vẽ hình trên giấy để cải thiện khả năng này.
Vẽ hình chính xác
Vẽ hình đúng và rõ ràng là bước quan trọng giúp bạn theo dõi các bước giải và tránh nhầm lẫn. Luyện tập vẽ hình nhiều lần và sử dụng thước kẻ và các dụng cụ vẽ để đảm bảo tính chính xác. Hãy làm quen với các cách biểu diễn hình học không gian trên giấy hai chiều.

Làm nhiều bài tập
Thực hành làm bài tập giúp bạn áp dụng lý thuyết vào thực tế và làm quen với nhiều dạng bài khác nhau. Làm bài tập trong sách giáo khoa và tìm thêm bài tập trên mạng hoặc trong các sách tham khảo. Chú ý giải thích chi tiết từng bước để nắm vững cách giải.
Chọn sách tham khảo phù hợp
Sách tham khảo tốt cung cấp nhiều bài tập phong phú và các phương pháp giải hay. Tham khảo ý kiến của giáo viên, bạn bè hoặc tìm kiếm các đánh giá sách để chọn được sách phù hợp với trình độ và nhu cầu của mình.
Cố gắng tìm bằng được đáp án
Tìm ra đáp án đúng giúp bạn kiểm tra được khả năng hiểu bài và phát hiện ra những sai sót trong quá trình giải. Nếu gặp bài tập khó, hãy cố gắng suy nghĩ và thử nhiều phương pháp khác nhau trước khi xem đáp án. Thảo luận với bạn bè hoặc hỏi thầy cô nếu cần.
Học cách phân tích đề hình học không gian
Phân tích đề giúp bạn hiểu rõ yêu cầu của bài và lập kế hoạch giải một cách hợp lý. Đọc kỹ đề bài, xác định các dữ liệu đã cho và cần tìm. Lập dàn ý các bước giải trước khi bắt đầu.

Kiên trì giải từng dạng đề khác nhau
Mỗi dạng đề có các phương pháp giải đặc thù. Kiên trì luyện tập giúp bạn nắm vững nhiều kỹ năng khác nhau. Chia bài tập thành các dạng khác nhau và giải từng dạng một cách kiên trì. Ghi chép lại các phương pháp giải và các lưu ý quan trọng.
Nguyên tắc giúp bạn vẽ hình chuẩn
Để vẽ hình học không gian một cách chính xác và hiệu quả, cần tuân thủ một số nguyên tắc cơ bản sau:
- Khi biểu diễn trên mặt phẳng ngang, các mặt phẳng nên được vẽ dưới dạng hình bình hành hoặc elip.
- Vẽ các đường thẳng vuông góc với mặt phẳng phải tuân theo hướng vuông góc với các cạnh của hình bình hành.
- Sử dụng nét đứt để biểu diễn các cạnh bị khuất sau các mặt phẳng khác.
- Đảm bảo đọc kỹ đề bài và phác thảo nháp trước khi vẽ hình cuối cùng.
Hướng dẫn cách vẽ các hình cơ bản:
- Hình Hộp: Vẽ các mặt đáy dưới dạng hình chữ nhật hoặc hình vuông, sau đó kết nối các đỉnh tương ứng trên mặt đáy và mặt trên bằng các đường thẳng đứng.
- Hình Chóp: Vẽ một đáy dưới dạng đa giác, tiếp tục vẽ đỉnh chóp và nối đỉnh này với các đỉnh của đáy bằng các đường thẳng.
- Hình Cầu: Biểu diễn mặt cầu bằng hai đường tròn lồng vào nhau, một đường thẳng nằm ngang qua tâm đường tròn đại diện cho đường kính.
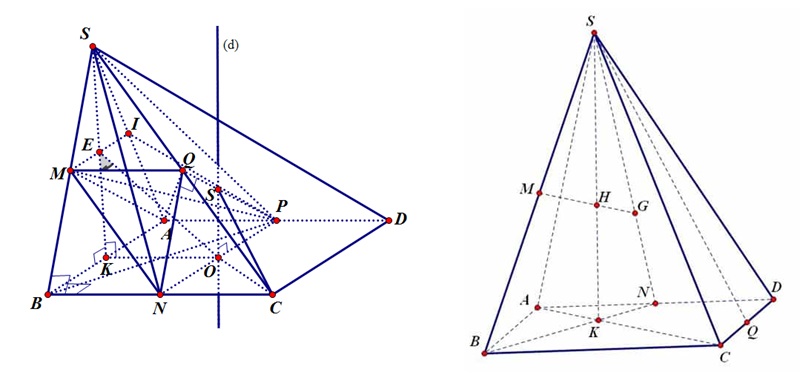
Áp dụng các quy tắc và mẹo này sẽ giúp bạn vẽ các hình không gian dễ dàng và chính xác hơn. Thực hành thường xuyên và áp dụng đúng các nguyên tắc này sẽ cải thiện đáng kể kỹ năng vẽ hình học không gian của bạn.
Khi vẽ hình học không gian, bạn hãy lưu ý đến các tính chất sau đây để hình vẽ dễ hiểu, thẩm mỹ hơn:
- Tính chính xác: Đảm bảo rằng các đối tượng trong hình học không gian được vẽ đúng kích thước và hình dạng.
- Phối cảnh: Áp dụng các quy tắc phối cảnh đúng cách để biểu diễn chiều sâu và không gian, giúp hình vẽ thể hiện được không gian ba chiều.
- Tỉ lệ: Duy trì tỷ lệ chính xác giữa các đối tượng, đặc biệt khi so sánh với các hình khác trong cùng không gian.
Các bước vẽ cơ bản bao gồm:
- Khởi tạo ý tưởng: Xác định rõ mục đích và nội dung cần vẽ, sau đó phác thảo sơ bộ.
- Lựa chọn hình dạng cơ bản: Xác định các hình dạng cơ bản như hình trụ, hình cầu, hình hộp để dễ dàng xây dựng hình.
- Phác thảo chi tiết: Sử dụng bút chì để phác thảo chi tiết từng phần của hình dựa trên các nguyên tắc đã nêu.
- Tô màu và hoàn thiện: Sử dụng màu sắc phù hợp để làm nổi bật hình vẽ và kiểm tra lại các chi tiết để đảm bảo tính chính xác và thẩm mỹ.
Ngoài ra, để vẽ tốt hơn bạn có thể tham khảo hình ảnh của người khác. Bạn hãy hỏi thầy cô bạn bè cách vẽ từng bước của một hình như thế nào rồi thực hành vẽ theo họ. Sau đó bạn cần hiểu thứ tự và tại sao lại vẽ như thế. Thực hành vẽ nhiều lần bạn sẽ dần quen và có thể tự vẽ hình vừa đẹp, vừa chuẩn xác.
Các dạng đề thường gặp khi giải hình học không gian
Khi bạn tìm hiểu làm sao để giỏi hình học không gian thì không thể bỏ qua phần lý thuyết căn bản. Những kiến thức nền tảng trong toán học là rất quan trọng. Vì bạn hiểu những thứ nhỏ nhặt bên dưới, mới có thể tiếp tục phát triển lên các bài toán khó. Dưới đây là một số dạng đề thường gặp khi giải hình học không gian, bạn hãy nắm vững khi giải bài tập.
Dạng 1: Tìm giao tuyến giữa hai mặt phẳng
Để tìm giao tuyến của hai mặt phẳng, bạn có thể sử dụng một trong hai phương pháp sau:
Phương pháp 1: Tìm 2 điểm chung giữa hai mặt phẳng đã cho:
- Điểm chung thứ nhất: Thường là điểm chung dễ thấy hoặc được cho sẵn trong đề bài.
- Điểm chung thứ hai: Xác định một đường thẳng trên mỗi mặt phẳng sao cho cả hai đường này nằm trên một mặt phẳng thứ ba và không song song với nhau. Giao điểm của hai đường thẳng này chính là điểm chung cần tìm.
- Nối hai điểm chung lại: Đường thẳng nối hai điểm chung này chính là giao tuyến của hai mặt phẳng.
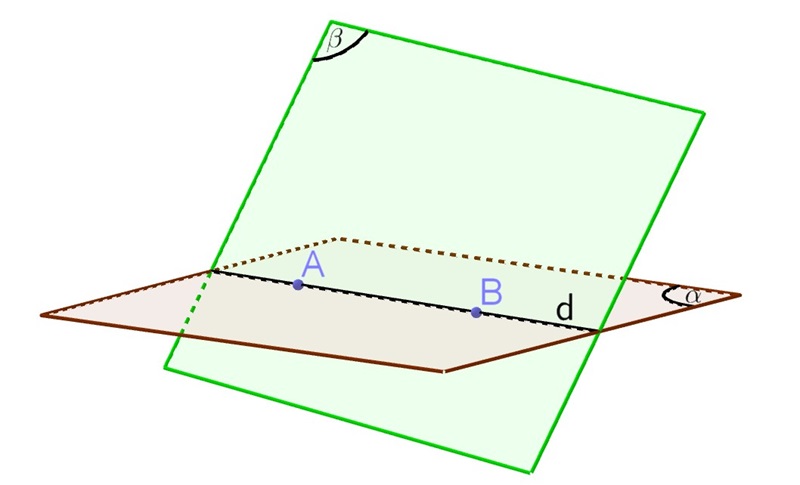
Phương pháp 2: Nếu hai mặt phẳng chứa hai đường thẳng song song:
- Xác định điểm chung: Tìm một điểm chung giữa hai mặt phẳng.
- Đường thẳng song song: Giao tuyến cần tìm sẽ là đường thẳng đi qua điểm chung này và song song với hai đường thẳng đã cho.
Áp dụng đúng các phương pháp này sẽ giúp bạn tìm được giao tuyến của hai mặt phẳng một cách chính xác.
Dạng 2: Tìm giao điểm của 1 đường thẳng d và mặt phẳng (α)
Để tìm giao điểm của một đường thẳng d và mặt phẳng (α) trong hình học không gian, bạn cần xác định giao điểm của đường thẳng d với một đường thẳng b thuộc mặt phẳng (α) Nếu chưa xác định được đường thẳng bbb, bạn có thể thực hiện các bước sau:
- Bước 1: Xác định một mặt phẳng (β) chứa đường thẳng d
- Bước 2: Tìm giao tuyến b giữa hai mặt phẳng (α)và (β)
- Bước 3: Xác định giao điểm giữa đường thẳng d và giao tuyến b
Bằng cách thực hiện đúng các bước này, bạn sẽ tìm được giao điểm của đường thẳng d và mặt phẳng (α)
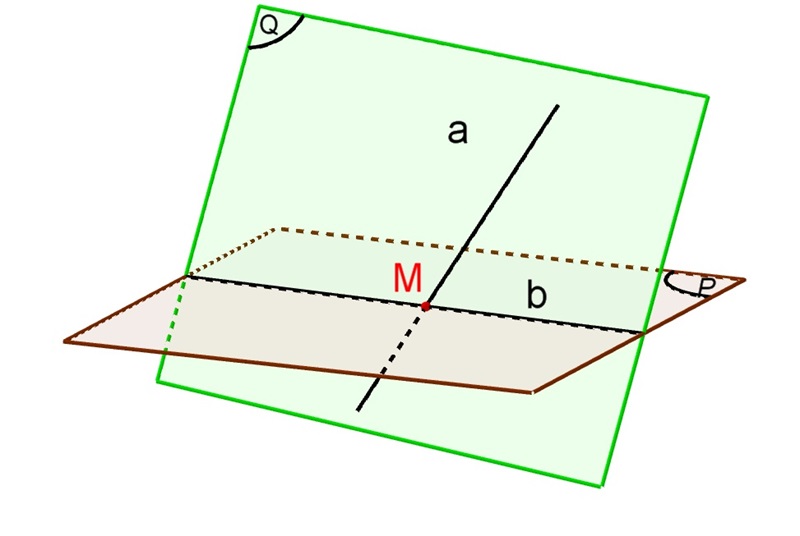
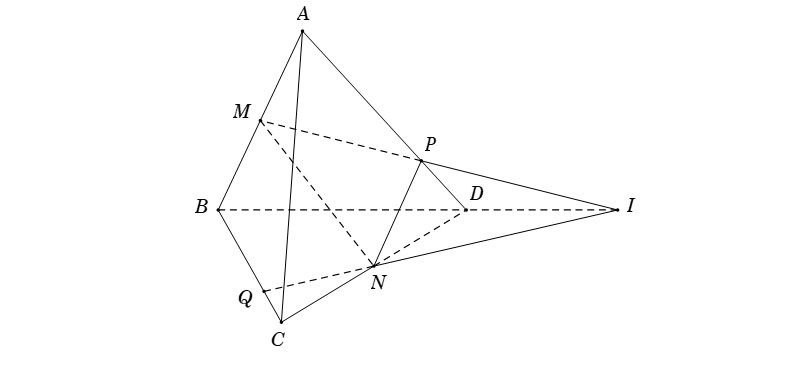
Dạng 3: Chứng minh 3 điểm cùng nằm trên một đường thẳng
Muốn chứng minh 3 điểm cùng nằm trên một đường thẳng trong hình học không gian, bạn cần chứng minh rằng chúng cùng nằm trên giao tuyến của 2 mặt phẳng riêng biệt.
Dạng 4: Chứng minh 3 đường thẳng đồng quy
Khi gặp dạng toán chứng minh 3 đường thẳng đồng quy trong hình học không gian thì bạn có thể áp dụng 2 hướng giải sau đây:
Cách 1: Tìm giao điểm của 2 đường thẳng nằm trên 2 mặt phẳng riêng biệt, rồi chứng minh rằng giao tuyến của 2 mặt phẳng này chính là đường thẳng thứ 3.
Cách 2: Xác định 3 mặt phẳng sao cho mỗi đường thẳng thuộc 3 mặt phẳng riêng biệt. Sau đó chứng minh 3 đường thẳng này cắt nhau từng đôi một.
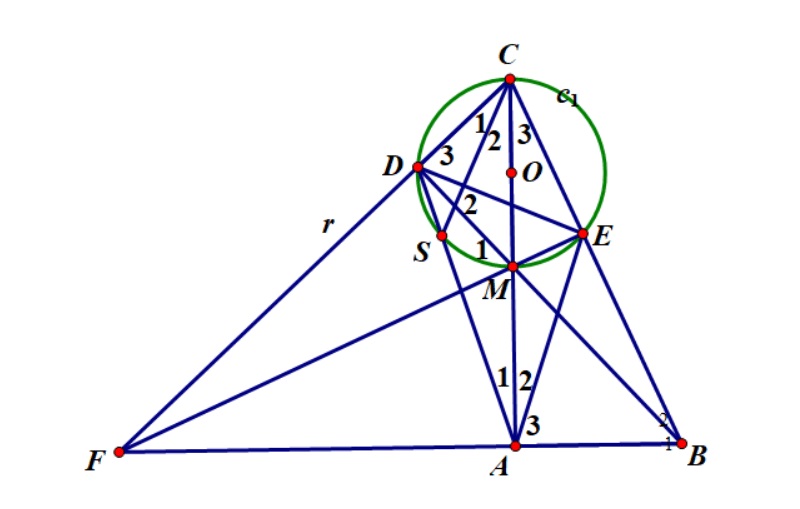
Bài Tập Rèn Luyện Dạng Toán Chứng Minh 3 Đường Thẳng Đồng Quy
Dạng 5: Chứng minh đường thẳng d song song với mặt phẳng (α)
Cách để chứng minh đường thẳng d song song với mặt phẳng (α) thì bạn có thể áp dụng 1 trong 2 cách sau đây:
Cách 1: Chứng minh đường thẳng d song song với một đường thẳng d’ bất kỳ thuộc mặt phẳng (α). Nếu đề bài chưa cho đường thẳng d’ thì hãy tìm bằng phương pháp sau đây.
- Bước 1: Tìm một mặt phẳng (β) chứa đường thẳng d nhưng không song song với (α).
- Bước 2: Xác định đường thẳng d’ là giao điểm của mặt phẳng (α) và (β).
- Bước 3: Chứng minh đường thẳng d song song với d’.
Cách 2: Chứng minh d thuộc mặt phẳng (β) và (β) song song với mặt phẳng (α)
BÀI TẬP HÌNH HỌC KHÔNG GIAN LỚP 11 CÓ LỜI GIẢI
Như vậy qua bài viết này bạn đã giải đáp được thắc mắc làm sao để giỏi hình học không gian rồi đúng không nào. Hãy lưu lại bài viết này và chia sẻ với những người cần đến để họ biết được bí quyết giỏi hình học không gian. Chúc bạn vui khỏe và học tốt.
Có thể bạn quan tâm:
- Đáp Án Đề Thi Ngữ Văn Tốt Nghiệp THPT Quốc Gia 2024? Hướng Dẫn Giải Đề Văn 2024 Chi Tiết
- Bật Mí Kinh Nghiệm Học Tốt Môn Toán – Giải Pháp Hữu Hiệu Chữa Dốt Toán
- Sách Tuyển Chọn 10 Năm Toán Tuổi Thơ THCS
- Tổng Hợp 9+ Đề Toán Tuổi Thơ Lớp 3 Các Trường Có Lời Giải

